Projects
This page first presents a selection of public coding projects, followed by my related research projects in quantum information theory and mathematical physics.Algorithms, Simulations & Web Code
Research Projects
Instantaneous Sobolev Regularization for Dissipative Bosonic Dynamics
We investigate quantum Markov semigroups on bosonic Fock space and identify a broad class of infinite-dimensional dissipative evolutions that exhibit instantaneous Sobolev-regularization. Motivated by stability problems in quantum computation, we show that for certain Lindblad operators that are polynomials of creation and annihilation operators, the resulting dynamics immediately transform any initial state into one with finite expectation in all powers of the number operator. A key application is in the bosonic cat code, where we obtain explicit estimates in the trace norm for the speed of convergence. These estimates sharpen existing perturbative bounds at both short and long times, offering new analytic tools for assessing stability and error suppression in bosonic quantum information processing. For example, we improve the strong exponential convergence of the (shifted) -photon dissipation to its fixed point to the uniform topology.
Learning and certification of local time-dependent quantum dynamics and noise
Hamiltonian learning protocols are essential tools to benchmark quantum computers and simulators. Yet rigorous methods for time-dependent Hamiltonians and Lindbladians remain scarce despite their wide use. We close this gap by learning the time-dependent evolution of a locally interacting $n$-qubit system on a graph of effective dimension $D$ using only preparation of product Pauli eigenstates, evolution under the time-dependent generator for given times, and measurements in product Pauli bases. We assume the time-dependent parameters are well approximated by functions in a known space of dimension m admitting stable interpolation, e.g. by polynomials. Our protocol outputs functions approximating these coefficients to accuracy $\epsilon$ on an interval with success probability $1-\delta$, requiring only $O\big(\epsilon^{-2}poly(m)\log(n\delta^{-1})\big)$ samples and $poly(n,m)$ pre/postprocessing. Importantly, the scaling in m is polynomial, whereas naive extensions of previous methods scale exponentially. The method estimates time derivatives of observable expectations via interpolation, yielding well-conditioned linear systems for the generator's coefficients. The main difficulty in the time-dependent setting is to evaluate these coefficients at finite times while preserving a controlled link between derivatives and dynamical parameters. Our innovation is to combine Lieb-Robinson bounds, process shadows, and semidefinite programs to recover the coefficients efficiently at constant times. Along the way, we extend state-of-the-art Lieb-Robinson bounds on general graphs to time-dependent, dissipative dynamics, a contribution of independent interest. These results provide a scalable tool to verify state-preparation procedures (e.g. adiabatic protocols) and characterize time-dependent noise in quantum devices.
Learning Coulomb Potentials and Beyond with Fermions in Continuous Space
We present a modular algorithm for learning external potentials in continuous-space free-fermion models including Coulomb potentials in any dimension. Compared to the lattice-based approaches, the continuum presents new mathematical challenges: the state space is infinite-dimensional and the Hamiltonian contains the Laplacian, which is unbounded in the continuum and thus produces an unbounded speed of information propagation. Our framework addresses these difficulties through novel optimization methods or information-propagation bounds in combination with a priori regularity assumptions on the external potential. The resulting algorithm provides a unified and robust approach that covers both Coulomb interactions and other classes of physically relevant potentials. One possible application is the characterization of charge and position of nuclei and ions in quantum chemistry. Our results thus lay the foundation for a scalable and generalizable toolkit to explore fermionic systems governed by continuous-space interactions.
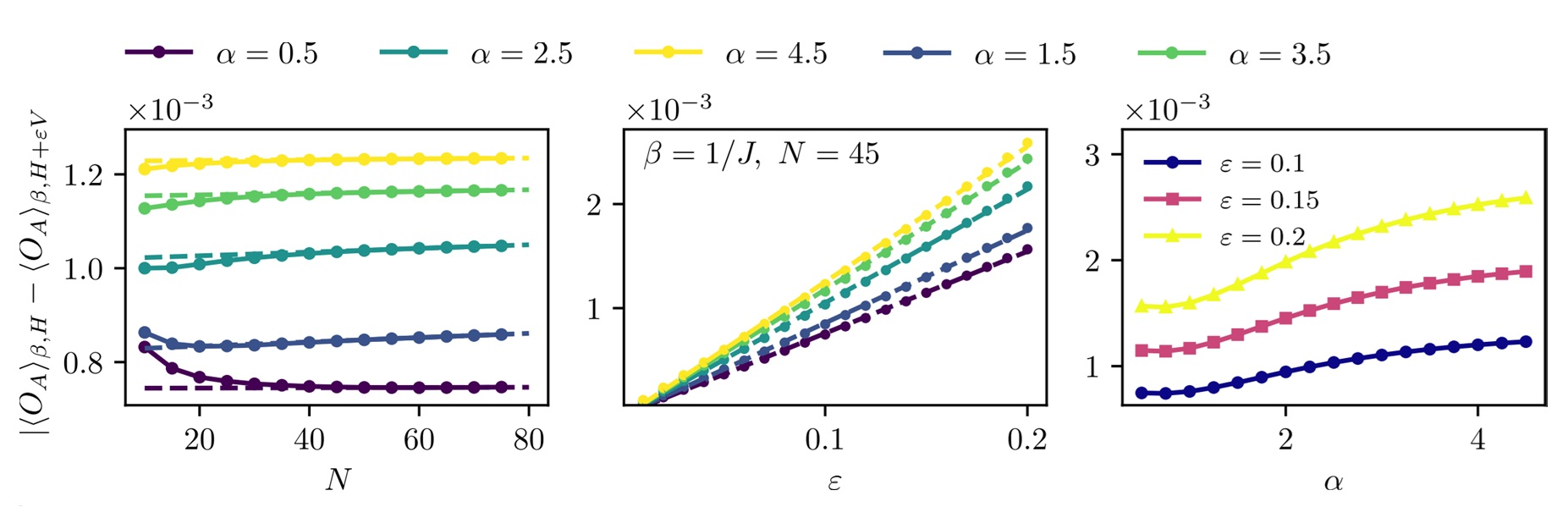
Stability of thermal equilibrium in long-range quantum systems
Experimental realizations of spin models are irremediably prone to errors, which can propagate through the system corrupting experimental signals. We study how such errors affect the measurement of local observables in systems with long-range interactions, where perturbations can spread more rapidly. Specifically, we focus on the stability of thermal equilibrium and investigate its relation to the correlation structure of the system, both analytically and numerically. As a main result, we prove that the stability of local expectation values follows from the decay of correlations on the Gibbs state and the Lieb-Robinson bound, and hence that stability always holds at high temperature. We also provide numerical evidence that this stability extends to an even larger regime of interacting long-range systems. Our results support the robustness of analogue simulation platforms for long-range models, and provide further evidence that computing physical quantities of interest can be significantly easier than performing arbitrary quantum computations.
Heisenberg-limited Hamiltonian learning continuous variable systems via engineered dissipation
Discrete and continuous variables oftentimes require different treatments in many learning tasks. Identifying the Hamiltonian governing the evolution of a quantum system is a fundamental task in quantum learning theory. While previous works mostly focused on quantum spin systems, where quantum states can be seen as superpositions of discrete bit-strings, relatively little is known about Hamiltonian learning for continuous-variable quantum systems. In this work we focus on learning the Hamiltonian of a bosonic quantum system, a common type of continuous-variable quantum system. This learning task involves an infinite-dimensional Hilbert space and unbounded operators, making mathematically rigorous treatments challenging. We introduce an analytic framework to study the effects of strong dissipation in such systems, enabling a rigorous analysis of cat qubit stabilization via engineered dissipation. This framework also supports the development of Heisenberg-limited algorithms for learning general bosonic Hamiltonians with higher-order terms of the creation and annihilation operators. Notably, our scheme requires a total Hamiltonian evolution time that scales only logarithmically with the number of modes and inversely with the precision of the reconstructed coefficients. On a theoretical level, we derive a new quantitative adiabatic approximation estimate for general Lindbladian evolutions with unbounded generators. Finally, we discuss possible experimental implementations.
Limits of Approximation of Quantum Markov Semigroups in Infinite-Dimensional Systems
This thesis explores the quantum Zeno effect and the Lie-Trotter product formula on infinite-dimensional quantum mechanical systems, for which optimal and explicit error bounds are proven. Furthermore, we establish sufficient conditions under which a bosonic initial value problem defines a unique quantum time evolution and possesses specific properties, which allows us to derive error bounds for the aforementioned product formula as well as the stability of fixed points. These results find applications in the bosonic cat code and the simulation of local time evolutions.
Multi-product Zeno effect with higher order convergence rates
To implement the dynamics of a projected Hamiltonian or Lindbladian, the quantum Zeno effect is a fundamental quantum phenomenon that approximates the effective dynamic by intersecting the Hamiltonian or Lindblad evolution by any quantum operation that converges to the desired projected subspace. Unlike the related Trotter product formula, the best-known convergence rate of the quantum Zeno effect is limited to the order $1/n$. In this work, we improve the convergence rate using a multi-product formula to achieve any power of $1/n^{K+1}$, employing a modified Chernoff Lemma, a modified Dunford-Segal approximation, and the holomorphic functional calculus. We briefly illustrate this scheme using the bosonic cat code as an example, along with a broader class of cases governed by the `Bang-Bang' method for decoupling systems from their environment.
Energy preserving evolutions over Bosonic systems
The exponential convergence to invariant subspaces of quantum Markov semigroups plays a crucial role in quantum information theory. In this paper, we investigate perturbations of quantum dynamical semigroups operating on continuous variable (CV) systems that admit an invariant subspace. To establish this analysis on mathematically sound foundations, we first prove a generation theorem for quantum Markov semigroups on CV systems under physically motivated assumptions about the generator structure.
Unified framework for continuity of sandwiched Rényi divergences
In this work, we prove uniform continuity bounds for entropic quantities related to the sandwiched Rényi divergences such as the sandwiched Rényi conditional entropy. We follow three different approaches: The first one exploits the sub-/superadditivity and joint concavity/convexity of the exponential of the divergence while the second uses norm-like properties of a power of the exponential inspired by norms on interpolation spaces. The third approach mixes the former two to achiev favourable scaling in all parameter regimes.
On Strong Bounds for Trotter and Zeno Product Formulas with Bosonic Applications
The Trotter product formula and the quantum Zeno effect are both indispensable tools for constructing time-evolutions using experimentally feasible building blocks. In this work, we discuss assumptions under which quantitative bounds can be proven in the strong operator topology on Banach spaces and provide natural bosonic examples. Specially, we assume the existence of a continuously embedded Banach space, which relatively bounds the involved generators and creates an invariant subspace of the limiting semigroup with a stable restriction. The slightly stronger assumption of admissible subspaces is well-recognized in the realm of hyperbolic evolution systems (time-dependent semigroups), to which the results are extended. By assuming access to a hierarchy of continuously embedded Banach spaces, Suzuki-higher-order bounds can be demonstrated. In bosonic applications, these embedded Banach spaces naturally arise through the number operator, leading to a diverse set of examples encompassing notable instances such as the Ornstein-Uhlenbeck semigroup and multi-photon driven dissipation used in bosonic error correction.
Dissipation-enabled bosonic Hamiltonian learning via new information-propagation bounds
Reliable quantum technology requires knowledge of the dynamics governing the underlying system. This problem of characterizing and benchmarking quantum devices or experiments in continuous time is referred to as the Hamiltonian learning problem. In contrast to multi-qubit systems, learning guarantees for the dynamics of bosonic systems have hitherto remained mostly unexplored. For -mode Hamiltonians given as polynomials in annihilation and creation operators with modes arranged on a lattice, we establish a simple moment criterion in terms of the particle number operator which ensures that learning strategies from the finite-dimensional setting extend to the bosonic setting, requiring only coherent states and heterodyne detection on the experimental side. We then propose an enhanced procedure based on added dissipation that even works if the Hamiltonian time evolution violates this moment criterion: With high success probability it learns all coefficients of the Hamiltonian to accuracy $\varepsilon$ using a total evolution time of $\mathcal{O}(\varepsilon^{-2}\log(m)$. Our protocol involves the experimentally reachable resources of projected coherent state preparation, dissipative regularization akin to recent quantum error correction schemes involving cat qubits stabilized by a nonlinear multi-photon driven dissipation process, and heterodyne measurements. As a crucial step in our analysis, we establish our moment criterion and a new Lieb-Robinson type bound for the evolution generated by an arbitrary bosonic Hamiltonian of bounded degree in the annihilation and creation operators combined with photon-driven dissipation. Our work demonstrates that a broad class of bosonic Hamiltonians can be efficiently learned from simple quantum experiments, and our bosonic Lieb-Robinson bound may independently serve as a versatile tool for studying evolutions on continuous variable systems.
Optimal convergence rate in the quantum Zeno effect for open quantum systems in infinite dimensions
In open quantum systems, the quantum Zeno effect consists in frequent applications of a given quantum operation, e.g.~a measurement, used to restrict the time evolution (due e.g.~to decoherence) to states that are invariant under the quantum operation. In an abstract setting, the Zeno sequence is an alternating concatenation of a contraction operator (quantum operation) and a C_0-contraction semigroup (time evolution) on a Banach space. In this paper, we prove the optimal convergence rate of order $\tfrac{1}{n}$ of the Zeno sequence by proving explicit error bounds. For that, we derive a new Chernoff-type $\sqrt{n}$-Lemma, which we believe to be of independent interest. Moreover, we generalize the convergence result for the Zeno effect in two directions: We weaken the assumptions on the generator, inducing the Zeno dynamics generated by an unbounded generator and we improve the convergence to the uniform topology. Finally, we provide a large class of examples arising from our assumptions.
Quantum Zeno effect generalized
The quantum Zeno effect, in its original form, uses frequent projective measurements to freeze the evolution of a quantum system that is initially governed by a fixed Hamiltonian. We generalize this effect simultaneously in three directions by allowing open system dynamics, time-dependent evolution equations and general quantum operations in place of projective measurements. More precisely, we study Markovian master equations with bounded generators whose time dependence is Lipschitz continuous. Under a spectral gap condition on the quantum operation, we show how frequent measurements again freeze the evolution outside an invariant subspace. Inside this space the evolution is described by a modified master equation.